


 
 
 
 
 |
前頁では、幾何要素/表記要素フィーチャの文字について見ましたので今回はスプラインについて見てみます。
| 幾何要素/表記要素|スプライン |
|
※SXF Ver.3.1仕様書より |
| パラメータ | 型 | 説明 | 範囲 |
| Layer | Int | レイヤコード |
|
| Color | Int | 色コード |
|
| Type | Int | 線種コード |
|
| line_width | Int | 線幅コード |
|
| open_close | Int | 開閉区分:0:閉 1:開 |
|
| number | Int | 頂点数 | 3n+1 |
| X |
CArray
<double,
double> | X座標(配列) |
double(64bits)の
範囲(有効桁15桁) |
| Y |
CArray
<double,
double> | Y座標(配列) |
double(64bits)の
範囲(有効桁15桁) |
備考
・開閉区分は、曲線が閉じているかどうかのフラグである(ただし参考値)。フラグが0:閉であっても、始点と同じ座標値の終点を頂点として指定する必要がある。
・スプラインは3次のベジェ曲線を使用する。頂点はベジェ曲線の制御点を示す。
・3次のベジェ曲線は以下の式で導かれる。
P(t) = (X0(t)*Q0) + (X1(t)*Q1) + (X2(t)*Q2) + (X3(t)*Q3)
・ここで、
tはパラメータで範囲は (0≦t≦1)
Q0〜Q3は制御点
X0〜X3 は t の関数で
X0(t) = (1-t)3
X1(t) = 3t(1-t)2
X2(t) = 3(1-t)t2
X3(t) = t3 |
とあります。
見た通り、「スプライン」と言いながら実はベジェ曲線だったりします。ベジェ曲線は GDI/GDI+/Direct2Dにも描画命令はありますが、これはmm単位指定の線種表現が出来ませんので使用しません。上記の式より座標を算出して線分補間を行います。
という事は取り合えず置いておき、ベジェ曲線といっても上記はGDI等と同様の、通過点+制御点1+制御点2+通過点の連続による集合体となっていますが、CADソフトによっては、始点+制御点1+制御点2+・・・+制御点n+終点、の描画を行うものもあります。例えば、Jw_cadでのベジェ曲線作図もそのようになっています。
このベジェ曲線を表現するには、
P(t)=ΣBi,n(t)Pi
の計算をしないといけません。
また、4点連続指定のベジェ曲線だと指定の仕方によっては
のように折れてしまって、スプライン=滑らかな曲線にはならない可能性もあります。ただ、これは、利用者側が、このように作図したいのだから、このように指定したのだ、という場合も有り得る訳なのですが。
スプライン曲線には、色々な種類があります。例えば、GDI+に実装されているカーディナルスプライン(カーティシアンスプライン)もその1つです。スプライン関連の本を見ると、平滑化スプライン、周期スプライン、自然スプライン、Cスプライン、パラメトリックスプライン、リーゼンフェルトスプライン、Bスプライン、ユニフォームBスプライン(UBS)、ノンユニフォームBスプライン(NUBS)、ノンユニフォームレーショナルスプライン(NURBS)、等の色々な名称が見られます。そして難解な計算式がわさわさと示されています。
元々、スプラインという言葉自体は「滑らかな曲線」というだけで、具体的な計算式が定義されている訳ではありません。滑らかな曲線であれば何でもいいわけで、例えば、放物線(2次曲線)やサインカーブ等も滑らかな曲線です。なので、3点間を2次曲線で表して、その連続で表現するスプラインもありますし、4点間を3次曲線で表して、その連続で表現するスプラインもあります。ただ、この場合、n元連立方程式を解く必要があったりで作図するには結構しんどい処理とは言えます。
その点、ベジェ曲線は、というと、上記の式で、t値を0から1へ増やしていくだけで途中の点が簡単に算出出来ますので、非常に簡単に描画が出来るという利点があります。Bスプライン曲線は、ベジェ曲線を拡張したような感じのものですから、これも容易です。そして有名なNURBSは、ノットベクトルやウエイトというものが絡んできてややこしいですが、算出式が出来上がってしまえば曲線の描画そのものは然程難しくはないと思います。
ただ、ベジェ曲線にしろ、Bスプライン曲線にしろ、NURBSにしろ、制御点での指定が必要になっていますが、CADソフトの場合、制御点の指定は無い場合が多く、通過点の指定から制御点を計算で求めて、それを使って曲線を作図する、という場合が多く、この計算が結構難解だったりするのですが。
さて、これからCADソフトを作ろう、スプライン曲線の作図を実装しよう、という場合において、「SXFレベル2・ネイティブ」を重要視するのであれば、スプライン曲線=ベジェ曲線、或いは、スプライン曲線=Bスプライン曲線=ベジェ曲線での表現、として、その他のスプライン曲線は考慮しないでおくか、又は、データ変換時にはその他のスプライン曲線を線分補間すれば良いと割り切って実装するか、又は、「SXFレベル2・ネイティブ」は重視せず独自に実装するか、の選択をしないといけないでしょう。
仮に、制御点ではなく通過点指定でデータ表現をする場合、SXF保存時は制御点を算出して出せば良い、としても、SXF読み込み時、指定通過点データは無い訳ですから、それはそれで困る事になります。線分補間する場合も同様、曲線を再編集する際に問題となるでしょう。それはそれで仕方がないと割り切るのも1つの手法です。
さて、ここでは、上記「スプライン曲線」は、明らかに「ベジェ曲線」ですので、ベジェ曲線データとしてデータ登録・描画を行う事とします。
それではベジェ曲線のデータ構造を決めます。
| UnitData.pas |
type
・・・
TDataBezier = record // 幾何要素/表記要素|スプライン
exf : Boolean ; // 存在フラグ(True:有り False:無し)
Layer : Integer ; // レイヤ(1〜256)
Color : Integer ; // 色 (0:レイヤ色 1〜256)
Ltype : Integer ; // 線種 (0:レイヤ線種 1〜32)
line_width: Integer ; // 線幅 (0:レイヤ線幅 1〜16)
open_close : Integer; // 開閉区分:0:閉 1:開
sep : Integer ; // 頂点間分割数
Number : Integer ; // 頂点数
X : array of double ; // 頂点X座標
Y : array of double ; // 頂点Y座標
end;
TFukugoZukeiDef = record // 構造化要素|複合図形定義
exf : Boolean ; // 存在フラグ(True:有り False:無し)
name : string ; // 複合図形名
Flag : Integer ; // 種別フラグ
cnt : Integer ; // 配置数
・・・
mBez : array of TDataBezier; // 幾何要素|スプライン→ベジェ
mBezN : Integer ; // 数
mFzk : array of TDataFukugoZukei; // 構造化要素|複合図形配置
mFzkN : Integer ; // 数
end;
TDataClass = class
public
{ Public 宣言 }
・・・
dBez : array of TDataBezier; // 表記要素|スプライン→ベジェ
dBezN : Integer ; // 数
・・・ |
データ追加用の関数は
function AddDataBezier(s:string;lay,col,ltp,wid,sp,num:integer;
vx,vy:array of double) : Boolean; |
のようにします。線分・折線等と同様、最初に「データ追加先の複合図形名(幾何要素) null:用紙へ追加(表記要素)」を指定するようにしています。頂点数は 3n+1 個となるので、それに合うよう調整します。open_close値は内部で確認・設定します。
| UnitData.pas |
// ベジェ曲線 データ項目の追加登録
function TDataClass.AddDataBezier(s:string;lay,col,ltp,wid,sp,num:integer;vx,vy:array of double) : Boolean;
var
m,i : integer ;
oc : integer ;
begin
Result := False;
if (lay < 1) or (lay > zLayN) then lay := 1 ;
if (col < 0) or (col > zColN) then col := 0 ;
if (ltp < 0) or (ltp > zLtpN) then ltp := 0 ;
if (wid < 0) or (wid > zWidN) then wid := 0 ;
if (sp < 1) then sp := 1 ;
if (sp > 1000) then sp := 1000 ;
if ( ((num-1)mod 3) > 0) then num := ((num-1) div 3)*3+1;
if (num <= 1) then exit ;
for i:=1 to num-1 do
if (((i-2) mod 3) > 0)
and(Abs(vx[i]-vx[i-1]) < LIMIT10)
and(Abs(vy[i]-vy[i-1]) < LIMIT10) then exit ; // 同一点
oc := 1;
if (Abs(vx[0]-vx[num-1]) < LIMIT10)
and(Abs(vy[0]-vy[num-1]) < LIMIT10) then oc := 0; // 閉
if (s = '') then begin
// 用紙へ追加
if (AddDataOrder(-1,9,dBezN)) then begin
try
Inc(dBezN);
if ((dBezN mod 100) = 1) then SetLength(dBez, dBezN+99);
with dBez[dBezN-1] do begin
exf := True ;
Layer := lay ;
Color := col ;
Ltype := ltp ;
line_width := wid ;
open_close := oc ;
sep := sp ;
Number := num ;
SetLength(X, num);
SetLength(Y, num);
for i:=0 to num-1 do begin
X[i] := vx[i];
Y[i] := vy[i];
end;
end;
Result := True ;
AddLayerCnt(lay,col,ltp,wid,-1);
except
Dec(dBezN);
Dec(dOrdN);
end;
end;
end
else begin
m := FZukeiNameCheck(0,s);
if (m = 0) then exit ; // 追加先の複合図形名は無いのでエラー
with fDef[m-1] do begin
if (AddDataOrder(m,9,mBezN)) then begin
try
Inc(mBezN);
if ((mBezN mod 100) = 1) then SetLength(mBez, mBezN+99);
with mBez[mBezN-1] do begin
exf := True ;
Layer := lay ;
Color := col ;
Ltype := ltp ;
line_width := wid ;
open_close := oc ;
sep := sp ;
Number := num ;
SetLength(X, num);
SetLength(Y, num);
for i:=0 to num-1 do begin
X[i] := vx[i];
Y[i] := vy[i];
end;
end;
Result := True ;
AddLayerFCnt(lay,col,ltp,wid,-1);
except
Dec(mBezN);
Dec(mOrdN);
end;
end;
end;
end;
end; |
これでベジェ曲線データの登録は出来るようになりました。
次に、ベジェ曲線の描画についてです。上記のSXF仕様書では X0(t)・X1(t)・X2(t)・X3(t) とありますが、これを変数 t0,t1,t2,t3 とすると
t = 0.0 → 1.0
t0 := (1.0-t)*(1.0-t)*(1.0-t);
t1 := 3.0*t*(1.0-t)*(1.0-t);
t2 := 3.0*(1.0-t)*t*t;
t3 := t*t*t;
と計算すれば良く、SXF仕様書では
P(t) = (X0(t)*Q0) + (X1(t)*Q1) + (X2(t)*Q2) + (X3(t)*Q3)
とありますので、座標計算は、
xp := (t0*x1) + (t1*x2) + (t2*x3) + (t3*x4);
yp := (t0*y1) + (t1*y2) + (t2*y3) + (t3*y4);
(x1,y1:始点、x2,y2:制御点1、x3,y3:制御点2、x4,y4:終点)
のようになります。これが1区間のベジェ曲線になります。これを連続して作図していけば良いです。
この1区間内を何分割するかを決め、t値を 0 から 1 へ変えます。例えば10分割とした場合は、t値を 0、0.1、0.2、0.3、・・・、0.9、1.0、と変えてその都度、t0・t1・t2・t3、xp,yp値を求めて、xp,yp間を結んでいけば、その1区間のベジェ曲線が作図出来ます。
| UnitDataGraph.pas |
// ベジェ曲線の表示 サブ
procedure DisplayBezierSub(var xp,yp:double;t,x1,x2,x3,x4, y1,y2,y3,y4:double);
var
t0,t1,t2,t3 : double ;
begin
t0 := (1.0-t)*(1.0-t)*(1.0-t);
t1 := 3.0*t*(1.0-t)*(1.0-t);
t2 := 3.0*(1.0-t)*t*t;
t3 := t*t*t;
xp := t0*x1 + t1*x2 + t2*x3 + t3*x4 ;
yp := t0*y1 + t1*y2 + t2*y3 + t3*y4 ;
end;
// ベジェ曲線の表示
procedure DisplayBezier(lay,col,ltp,wid,sp,num:integer;vx,vy:array of double);
var
c,cc,l,w, i,j,k : integer ;
ww, d1 ,t,x1,y1,x2,y2 : double ;
begin
DisplayLayCol2(lay,col,ltp,wid, c,cc,l,w,ww); // 色・線種・線幅
//
if (CData.zLtp[l-1].Segment = 0)
or(CData.zLtp[l-1].SpaceMax * mm_dot < 2.0)
or(CData.zLtp[l-1].SpaceMax * mm_dot < ww ) then begin
for j:=0 to ((num-1) div 3)-1 do begin
t := 0.0;
DisplayBezierSub(x1,y1, t,
vx[j*3],vx[j*3+1],vx[j*3+2],vx[j*3+3],
vy[j*3],vy[j*3+1],vy[j*3+2],vy[j*3+3]);
for k:=1 to sp do begin
t := t + 1.0/sp ;
DisplayBezierSub(x2,y2, t,
vx[j*3],vx[j*3+1],vx[j*3+2],vx[j*3+3],
vy[j*3],vy[j*3+1],vy[j*3+2],vy[j*3+3]);
DisplayLineSub1(x1,y1, x2,y2);
x1:= x2;
y1:= y2;
end;
end;
end
else begin
i := 0 ;
d1:= 0.0 ;
for j:=0 to ((num-1) div 3)-1 do begin
t := 0.0;
DisplayBezierSub(x1,y1, t,
vx[j*3],vx[j*3+1],vx[j*3+2],vx[j*3+3],
vy[j*3],vy[j*3+1],vy[j*3+2],vy[j*3+3]);
for k:=1 to sp do begin
t := t + 1.0/sp ;
DisplayBezierSub(x2,y2, t,
vx[j*3],vx[j*3+1],vx[j*3+2],vx[j*3+3],
vy[j*3],vy[j*3+1],vy[j*3+2],vy[j*3+3]);
DisplayLineSub2(l,i,d1, x1,y1, x2,y2);
x1:= x2;
y1:= y2;
end;
end;
end;
end; |
簡単なテストを Unit1.pas に記述して、再構築(コンパイル)し実行してみます。
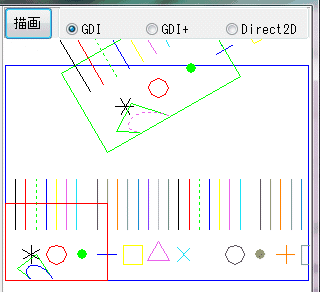
分割数を少なくすると、ベジェ曲線は粗くなります。分割数を多くするとベジェ曲線は綺麗に見えます。ベジェ曲線要素として登録していますので、線分データが増える訳ではありませんので、分割数を多くしてもデータは巨大化しません。しかし、DXFで他CADへデータを受け渡す場合には、線分データの集まりとしてファイル保存を行うためにファイルサイズは大きくなるでしょうし、交点計算等を行う場合は各補間線分との交点計算をせざるを得ないため分割数が多いと計算量も多くなるため、その分、遅くなるであろうと考えられます。
それでは、ここまでのテストプログラムです。実行ファイル、gdiplus.dll、gdipフォルダは入っていません。ソースのみです。
|
|
CAD装置(1)
CAD装置(2)
メディア
AutoCADの
DIESELマクロ
CSV
DXF
PCES
IGES
STEP
数学とCAD
CAD作ろ!
CADを考える
▲PREV
▼NEXT
M7
Jw_cad
|



