


 
 
 
 
 |
仛嶰妏宍
仠嶰妏宍偺崌摨忦審
侾乯俁曈偑摍偟偄
俀乯俀曈偲偦偺偼偝傓妏偑摍偟偄
俁乯侾曈偲偦偺椉抂偺妏偑摍偟偄
仠擇摍曈嶰妏宍丂丗丂俀曈偑摍偟偄嶰妏宍
侾乯俀偮偺掙妏偑摍偟偄
俀乯捀妏偺俀摍暘慄偼掙曈傪悅捈偵俀摍暘偡傞
仠惓嶰妏宍丂丗丂俁曈偑摍偟偄嶰妏宍
侾乯俁偮偺妏偼慡偰60亱偱摍偟偄
仠捈妏嶰妏宍偺崌摨忦審
侾乯幬曈偲侾塻妏偑摍偟偄
俀乯幬曈偲懠偺侾曈偑摍偟偄
丂
仠柺愊
 |
俽亖倎亊倛乛俀
丂
僿儘儞偺岞幃
倱亖乮倎亄倐亄們乯乛俀
俽亖併(倱(倱亅倎)(倱亅倐)(倱亅們))
丂
俽亖乮倐們sin俙乯乛俀
丂亖乮們倎sin俛乯乛俀
丂亖乮倎倐sin俠乯乛俀 |
丂
仛嶰妏宍偺憡帡忦審
侾乯俁慻偺曈偺斾偑慡偰摍偟偄
丂俙俛丗倎倐亖俛俠丗倐們亖俠俙丗們倎
丂俙俛乛倎倐亖俛俠乛倐們亖俠俙乛們倎
俀乯俀慻偺曈偺斾偑摍偟偔丄偦偺偼偝傓妏偑摍偟偄
丂俙俛丗倎倐亖俛俠丗倐們
丂丂丂俙俛乛倎倐亖俛俠乛倐們
丂佢俛亖佢倐
俁乯俀慻偺妏偑偦傟偧傟摍偟偄
丂佢俛亖佢倐丄佢俠亖佢們
丂
仛嶰妏宍偲暯峴慄
 |
俢俤//俛俠側傜偽
嘆俙俛:俙俢亖俙俠:俙俤亖俛俠:俢俤
丂俙俛/俙俢亖俙俠/俙俤亖俛俠/俢俤
嘇俙俢:俢俛亖俙俤:俤俠
丂俙俢/俢俛亖俙俤/俤俠
丂
嘆俙俛:俙俢亖俙俠:俙俤
丂俙俛/俙俢亖俙俠/俙俤丂側傜偽
丂丂丂俢俤//俛俠
嘇俙俢:俢俛亖俙俤:俤俠
丂俙俢/俢俛亖俙俤/俤俠丂側傜偽
丂丂丂俢俤//俛俠 |
丂
仛拞揰楢寢掕棟
 |
嘆嶰妏宍偺俀曈偺拞揰傪寢傇慄暘偼丄巆傝偺曈偵暯峴偱丄挿偝偼偦偺敿暘偵摍偟偄丄
俙俢亖俢俛丆俙俤亖俤俠
丂仺
丂丂俢俤//俛俠丆俢俤亖俛俠乛俀
丂
嘇嶰妏宍偺侾偮偺曈偺拞揰傪捠傝丄懠偺曈偵暯峴側捈慄偼丄巆傝偺曈偺拞揰傪捠傞丅
俙俢亖俢俛丆俢俤//俛俠
丂仺
丂丂俙俤亖俤俠 |
丂
仛嶰妏宍偺廳怱
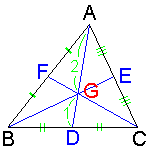 |
嘆嶰妏宍偺俁偮偺拞慄偼侾揰偱岎傢傞丅偙傟傪廳怱偲偄偆丅
嘇廳怱偼俁偮偺拞慄傪偦傟偧傟捀揰偺曽偐傜俀丗侾偵暘偗傞丅
丂俙俧丗俧俢
丂亖俛俧丗俧俤
丂丂亖俠俧丗俧俥丂亖丂俀丗侾
偡側傢偪
俙俧/俧俢亖俛俧/俧俤亖俠俧/俧俥亖俀 |
丂
仛妏偺擇摍暘慄偲曈偺斾
 |
嶰妏宍俙俛俠偺撪妏俙偺俀摍暘慄偑曈俛俠偲岎傢傞揰傪俢偲偡傞応崌
俙俛丗俙俠亖俛俢丗俢俠
偮傑傝
俙俛乛俙俠亖俛俢乛俢俠 |
丂
仛僠僃僶偺掕棟
 |
嶰妏宍俙俛俠撪偵揰俹偑偁傝丄俙俹丄俛俹丄俠俹偑懳曈偲岎傢傞揰傪奺乆俢丄俤丄俥偲偡傞応崌
|
丂
仛儊僱儔僂僗偺掕棟
 |
侾偮偺捈慄偑嶰妏宍俙俛俠偺曈俛俠丄俠俙丄俙俛枖偼偦傟傜偺墑挿偲岎傢傞揰傪奺乆俢丄俤丄俥偲偡傞応崌
|
丂
丂
|
|
CAD憰抲(1)
CAD憰抲(2)
儊僨傿傾
AutoCAD偺
DIESEL儅僋儘
俠俽倁
俢倃俥
俹俠俤俽
俬俧俤俽
俽俿俤俹
悢妛偲CAD
丂仯PREV
丂仴NEXT
CAD嶌傠両
丂 |



