


 
 
 
 
 |
崅峑悢妛偺婎慴乮俇乯偱彮偟彂偒傑偟偨偑丄偙偙偱偼傕偆彮偟徻偟偔婰弎偟偰偍偒傑偡丅
丂
墌偲墌偺岎揰寁嶼傪偡傞偺偵楢棫曽掱幃傪夝偔応崌丄憃曽偲傕俀師幃偱偁傞偨傔丄楢棫曽掱幃傪夝偔偺傕堦嬯楯偟偰偟傑偄傑偡丅偙偙偱傕夞揮幨憸傪棙梡偟偰夝偔帠傪峫偊傑偡丅
 |
嘆傑偢丄俀墌偺拞怱揰傪寢傇捈慄傪峫偊丄偦偺孹偒妏搙傪嶼弌偟傑偡丅
丂
A := ArcTan2(y2-y1,x2-x1); |
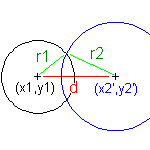 |
嘇揰(x1,y1)傪拞怱偵妏搙A暘丄媡夞揮偟偨偲峫偊傑偡丅
(x2,y2)偺夞揮屻偑(x2',y2')
偱偡丅
丂
嘊墌偺拞怱揰娫嫍棧倓傪寁嶼偟傑偡丅
丂丂嫍棧倓亖乥x2'亅x1乥
偙偺倓偑墌偺敿宎乮r1亄r2乯偵摍偟偄応崌偼丄俀墌偼愙偡傞帠偵側傝丄(r1亄r2)傛傝傕彫偝偄帪偵偼俀岎揰丄(r1亄r2)傛傝傕戝偒偄帪偼岎揰柍偟丄偲側傝傑偡丅
傑偨丄倓偑乥r1亅r2乥偵摍偟偄応崌偼丄俀墌偼撪愙偡傞帠偵側傝丄乥r1亅r2乥傛傝傕彫偝偄帪偼岎揰柍偟偲側傝傑偡丅摨怱墌偺応崌乮倓亖侽乯傕岎揰柍偟偲側傝傑偡丅
丂 |
 |
嘋愙偡傞応崌乮侾岎揰偱偁傞応崌乯丄r1亞r2 側傜偽 (x1+r1,y1)丄r1亙r2 側傜偽 (x1+d-br,y1)偲側傝傑偡丅
俀岎揰偺応崌偵偼丄
丂A亄B亖d丄A2亄h2亖r12丄B2亄h2亖r22
偙傟傛傝丄
丂A2亅B2亖r12亅r22
丂A2亅(d亅A)2亖r12亅r22
丂A2亅(d2亅2dA亄A2)亖r12亅r22
丂亅d2亄2dA亖r12亅r22
丂2dA亖d2亄r12亅r22
丂A亖(d2亄r12亅r22)乛2d
丂h亖併(r12亅A2)
偲側傝傑偡偺偱丄岎揰偼丄
丂(x1亄A,y1亇h)
偲側傝傑偡丅 |
 |
嘍愙揰枖偼岎揰傪
揰(x1,y1)傪拞怱偵妏搙A暘丄夞揮偟偨揰偺嵗昗偑丄媮傔傞揰偲側傝傑偡丅 |
丂
夞揮幨憸偼丄
 | 乮 | cos兤丂-sin兤 | 乯丂兤丗夞揮妏 |
| sin兤丂cos兤 |
偮傑傝
丂丂x'亖x亊cos兤亅y亊sin兤
丂丂y'亖x亊sin兤亄y亊cos兤
偱偡偑丄偙傟偼拞怱(0,0)偱偺夞揮偱偡偺偱丄揰(x0,y0)傪拞怱偵夞揮偡傞応崌偵偼丄
丂丂x'亖x0亄(x亅x0)亊cos兤亅(y亅y0)亊sin兤
丂丂y'亖y0亄(x亅x0)亊sin兤亄(y亅y0)亊cos兤
偲側傝傑偡丅
丂
| 夞揮幨憸傪棙梡偟偰丄俀墌偺岎揰傪昞帵偡傞娙扨側僒儞僾儖僾儘僌儔儉偱偡丅奊偼丄TImage傪攝抲偟偰丄偦偙偵昤偒傑偡丅10僪僢僩傪侾扨埵偲偟傑偡丅 |
丂
丂
|
|
CAD憰抲(1)
CAD憰抲(2)
儊僨傿傾
AutoCAD偺
DIESEL儅僋儘
俠俽倁
俢倃俥
俹俠俤俽
俬俧俤俽
俽俿俤俹
悢妛偲CAD
丂仯PREV
丂仴NEXT
CAD嶌傠両
丂 |



