


 
 
 
 
 |
三角関数については、既に前節等でも述べていますが、もう一度ここで確認のためにも記載しておきます。
 |
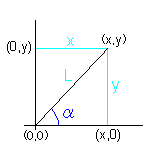
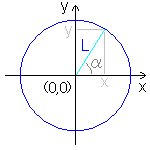 |
ピタゴラスの定理
x2+y2=L2
より、
L=√(x2+y2)
です。
三角関数は、以下のようになります。
sinα=y/L
cosα=x/L
tanα=y/x
つまり、
y=L×sinα
x=L×cosα
y=x×tanα
の関係になります。 |
よく利用される三角比には、以下のものがあります。
相互関係
| (1) 90°−Aの三角比 |
sin(90o−A)
=cosA |
cos(90o−A)
=sinA |
tan(90o−A)
=1/tanA |
| (2) 正接と正弦・余弦 |
| tanA=sinA/cosA (A≠90°) |
| (3) 正弦と余弦の平方の和 |
| sin2A+cos2A=1 |
正弦定理
 | 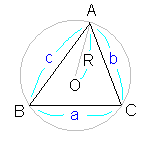 |
a/sinA=b/sinB=c/sinC=2R
R:△ABCの外接円の半径 |
余弦定理(第2余弦定理)
 | 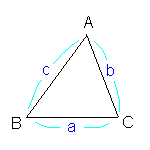 |
a2=b2+c2−2bccosA
b2=c2+a2−2cacosB
c2=a2+b2−2abcosC |
第1余弦定理
 |  |
a=bcosC+ccosB
b=ccosA+acosC
c=acosB+bcosA |
三角形の面積
逆三角関数
 |
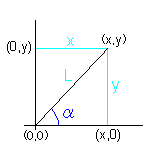
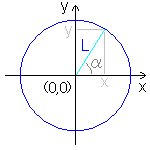 |
αが分かっていて、そのx、y、Lの各値を算出する場合には三角関数を利用すれば良いですが、逆に、x、y、Lの各値が分かっていて、αの値を知りたい場合には、逆三角関数を利用します。
α=sin-1(y/L)
α=cos-1(x/L)
α=tan-1(y/x)
Delphi6では、
アークサイン(sin-1)は、ArcSin()
アークコサイン(cos-1)は、ArcCos()
アークタンジェント(tan-1)は、ArcTan() 又は ArcTan2()
で求める事が出来ます。 |
仮に、tan-1はあるが、sin-1 や cos-1 が無い言語処理系の場合、「ピタゴラスの定理 x2+y2=L2」を利用して求める事になります。つまり、
α=sin-1(y/L)
=tan-1(y/√(L2−y2))
α=cos-1(x/L)
=tan-1(√(L2−x2)/x)
のようにして算出します。
|
|
CAD装置(1)
CAD装置(2)
メディア
AutoCADの
DIESELマクロ
CSV
DXF
PCES
IGES
STEP
数学とCAD
▲PREV
▼NEXT
CAD作ろ!
|



