


 
 
 
 
 |
前頁は構造化要素のハッチング(ユーザ定義)について考えてみましたので、今回は、ハッチング(パターン)について考えてみます。
ハッチング要素データ(パターン)は、SXF仕様書では以下のように記載されています。
| 構造化要素|ハッチング(パターン) |
|
※SXF Ver.3.1仕様書より |
| パラメータ | 型 | 説明 | 範囲 |
| Layer | Int | レイヤコード | |
| name[257] | Char | 既定義シンボル名 |
0<文字列長≦256
バイト |
| hatch_color | Int | ハッチパターンの色コード |
|
| hatch_pattern_x | double | ハッチパターン配置位置x座標 |
double(64bits)の
範囲(有効桁15桁) |
| hatch_pattern_y | double | ハッチパターン配置位置y座標 |
double(64bits)の
範囲(有効桁15桁) |
hatch_pattern
_vector1 | double | ハッチパターンの繰返しベクトル1の大きさ | 0<大きさ<1.0×1015 |
hatch_pattern
_vector1_angle | double | ハッチパターンの繰返しベクトル1の角度 | 0≦度<360 |
hatch_pattern
_vector2 | double | ハッチパターンの繰返しベクトル2の大きさ | 0<大きさ<1.0×1015 |
hatch_pattern
_vector2_angle | double | ハッチパターンの繰返しベクトル2の角度 | 0≦度<360 |
hatch_pattern
_scale_x | double | ハッチパターンのX尺度 | 0<尺度<1.0×1015 |
hatch_pattern
_scale_y | double | ハッチパターンのY尺度 | 0<尺度<1.0×1015 |
hatch_pattern
_angle | double | ハッチパターンの向きの角度 | 0≦度<360 |
| Out_id | Int | 外形の複合曲線のフィーチャコード | |
| number | Int | 中抜きの閉領域数 |
0≦数<int(32bits)
の最大値 |
| In_id |
CArray
<int,
int> | 中抜きの複合曲線のフィーチャコード(配列) | |
備考
・ハッチパターンの向きのx方向成分、向きのy方向成分はハッチパターンの向きの角度から計算する。
・繰返しベクトル1、2のX方向成分、Y方向成分はそれぞれの角度から計算する。
・ハッチパターンのスケール=ハッチパターンのx_scale=ハッチパターンのy_scaleとする。
・角度は水平右側が0度、反時計廻りが正、単位は度とする。 |
という風に記載されています。パラメータの名前で大文字・小文字が他のものと統一されていないようですし、こちらは「hatch_color」であって「hatch1_color」では無いようですが・・・。
まず最初の疑問は、配置位置がハッチング領域(外形)内になければならないのか、それとも、ハッチング領域(外形)外にあっても良いのか、という点です。ハッチングのロジックは、ある点から上へ走査して「作図無し」になれば次に下へ走査し、「作図無し」になるまで処理を行いますが、領域外になると、上へ走査するといきなり「作図無し」、下へ走査しても「作図無し」となって、ハッチング処理が行われない、という事になるためです。そのためハッチング(ユーザ定義)では、必ず「作図有り」になるよう新配置点の算出を行っていました。
ハッチング(パターン)の場合は、上下方向だけでなく、左右方向にも走査を行う必要があります。また、シンボルの基準点(0,0)が、シンボル図形の中心や左下にあるとは限りません。また、パターン=シンボル図形に尺度と回転も掛かります。そのため、注意が必要であろうと思われます。
そのため、指定したハッチパターン配置位置を基準として作図されるであろうパターン=シンボル図形の各データの座標点を、ハッチング図形領域の中心点に出来るだけ近づける計算が必要でしょう。
ハッチパターンの繰返しベクトル1・ベクトル2を別々に考えて、まずはベクトル1。データ点を中心としてベクトル1の角度分、ハッチング図形領域中心点を逆回転します。同じく、ベクトル2も同じ角度分逆回転させ、その高さを整数割り算したものが、ベクトル2側のパターン本数(n2)になります。ベクトル1・2を逆にすれば、ベクトル1側のパターン本数(n1)も分かります。但し、座標点の位置関係によってはマイナス値にもなりますので留意しておきます。
データ点(xp,yp)、新データ点(xn,yn)とすれば
x'=xp+hatch_pattern_vector2×n2×Cos(hatch_pattern_vector2_angle)
y'=yp+hatch_pattern_vector2×n2×Sin(hatch_pattern_vector2_angle)
xn=x'+hatch_pattern_vector1×n1×Cos(hatch_pattern_vector1_angle)
yn=y'+hatch_pattern_vector1×n1×Sin(hatch_pattern_vector1_angle)
で算出できます。
この新データ点によるパターン図形をハッチパターンベクトル分、プラス方向マイナス方向に繰り返せば、少なくとも線データによるシンボル図形をパターンとするハッチング(パターン)データの描画は可能になると思われます。
円・円弧・楕円・楕円弧・スプライン曲線などは線データに分解すると考えれば処理・描画は可能だと思われますが、文字等についてはどうするのか?等の問題は残ります。
こういった手法ではなく、パターンを画像化してしまい、画像ファイルによって塗り潰す処理を行う、という手法もあるかもしれません。
画像による塗り潰しは、GDIでは難しいですが、GDI+・Direct2Dの場合には容易に実現可能です。画像ファイルを一時的に生成する事も、おそらくそう難しくは無いでしょう。この表現方法で問題になりそうなのは、画面を拡大・縮小しても、画像状態はそのままのため、見え方が変わってくるという点です。同様の理由で、印刷時、解像度によって見え方が変わるという問題もあります。一時的画像ファイルを画面の拡大・縮小のたびに再生成をすれば変わってきますが、そうなると、画像サイズは余り大きく作れないための問題も生じますし、画像ファイルサイズも大きくなって処理が遅くなりますから、描画速度を要求され、尚且つ、かなりの拡大表示を行う CADソフトの場合には、使いにくい手法です。
ですのでこの手法では、ハッチング(パターン)要素データの各指定項目値を正確に表現するのはかなり難しくなってしまいます。
また、SXF仕様において、ハッチング(パターン)要素データで扱うパターンのシンボル図形では、どういったフィーチャ(図形要素)を対象としているのかが現状よく分かりません。SXFライブラリを使ってSXFファイルを作成し、実際に、SXFブラウザで確認してみる等の作業が必要でしょう。私自身、今現在(H23/11/27)はまだSXFライブラリを取得していません。SXFファイルを扱えるソフトウェアをまだ作成していないから、なのですが・・・。
という訳でここではまず、パターン=シンボル図形は、線データのみで構成される、と制限した上での、ハッチング(パターン)について考えていきます。
まずは、ハッチング(パターン)のデータ構造です。
| UnitData.pas |
type
・・・
TDataHatch4 = record // 構造化要素|ハッチング(パターン)
exf : Boolean ; // 存在フラグ(True:有り False:無し)
Layer : Integer ; // レイヤ(1〜256)
name : string ; // 既定義シンボル名
hatch_color : Integer ; // ハッチパターンの色
hatch_pattern_x : double ; // ハッチパターン配置位置X座標
hatch_pattern_y : double ; // ハッチパターン配置位置Y座標
hatch_pattern_vector1 : double ; // ベクトル1の大きさ
hatch_pattern_vector1_angle: double ; // ベクトル1の角度[°]
hatch_pattern_vector2 : double ; // ベクトル2の大きさ
hatch_pattern_vector2_angle: double ; // ベクトル2の角度[°]
hatch_pattern_scale_x : double ; // ハッチパターンのX尺度
hatch_pattern_scale_y : double ; // ハッチパターンのY尺度
hatch_pattern_angle : double ; // ハッチパターン角度[°]
out_id : Integer ; // 外形の複合曲線のフィーチャコード
Number : Integer ; // 中抜の閉領域数(0〜)
in_id : array of Integer; // 中抜の複合曲線のフィーチャコード
hln : integer ; // ハッチング線数
hl : array of THatchLine; // ハッチング線
end;
・・・ |
「ハッチパターンの色」についてですが、既定義シンボルフィーチャでは、color_flag:色コードフラグ(0:色コード無効、1:有効)という指定項目がありました。つまり、シンボル定義で各要素データ毎に指定される色で表示をするのか、既定義シンボルで指定される1色で表示をするのか、という事ですが、ハッチング(パターン)では、色コードフラグの指定というものがありません。いきなり「ハッチパターンの色コード」があるだけです。つまりこれは、シンボル定義での各要素データ毎の色は無視をして、ここで指定される色での描画を行う、と解釈するのが普通でしょう。
ハッチング(パターン)のデータ登録は下記のようにします。
| UnitData.pas |
// ハッチング(パターン) データ項目の追加登録
function TDataClass.AddDataHatch4(s,st:string;lay,col:integer;
px,py,pv1,pv1a,pv2,pv2a,psx,psy,pa:double;
oid,num:integer; iid:array of integer) : Boolean ; |
ハッチング(パターン)の描画については、ハッチング(既定義)要素・ハッチング(ユーザ定義)要素と同様、ハッチング線を算出してそれを描画するようにしますので、手続き DisplayHatch1 をそのまま利用します。
実際のハッチング計算は手続き MakeHatch4 にて行うようにします。ハッチング(既定義)・(ユーザ定義)要素データと同様、この手続きで算出したハッチング線を変数 zHLn,zHLnN を経由して hl,hln に登録し、実際のハッチング線の描画はこの hl,hln を参照するようにします。
| UnitData.pas |
// ハッチング(パターン) ハッチング線の算出
// n : パターン=シンボル図形 番号(-1〜)
// col : 線色コード
// px : ハッチパターン配置位置X座標
// py : ハッチパターン配置位置Y座標
// pv1 : ハッチパターンの繰返しベクトル1の大きさ
// pv1a : ハッチパターンの繰返しベクトル1の角度[°]
// pv2 : ハッチパターンの繰返しベクトル2の大きさ
// pv2a : ハッチパターンの繰返しベクトル2の角度[°]
// psx : ハッチパターンのX尺度
// psy : ハッチパターンのY尺度
// pa : ハッチパターンの向きの角度[°]
// (ret)
// zHLn, zHLnN
procedure TDataClass.MakeHatch4(n,col:integer;
px,py,pv1,pv1a,pv2,pv2a,psx,psy,pa:double) ;
var
tr,tr1 : TMatrix ;
i,o,o1,o2 : integer ;
wx1,wy1,wx2,wy2 : double ;
n1,n2,w1,w2,w3,w4,w5,w6,lx1,ly1,lx2,ly2 : double ;
ltp,wid : integer ;
begin
zHLn := nil ;
zHLnN:= 0 ;
if (n >= 0) then exit;
// min,maxを取得
with zHAr[0] do begin
wx1 := a[0].x ;
wy1 := a[0].y ;
wx2 := wx1;
wy2 := wy1;
for i:=1 to an-1 do begin
if (wx1 > a[i].x) then wx1 := a[i].x ;
if (wy1 > a[i].y) then wy1 := a[i].y ;
if (wx2 < a[i].x) then wx2 := a[i].x ;
if (wy2 < a[i].y) then wy2 := a[i].y ;
end;
end;
//
w5 := pv1a/180.0*Pi ;
w6 := pv2a/180.0*Pi ;
w1 := pv2*Cos(w6-w5);
w2 := pv2*Sin(w6-w5);
w3 := pv1*Cos(w5-w6);
w4 := pv1*Sin(w5-w6);
//
// 変換行列を作成
MtxScale(tr, psx,psy);
MtxRotD(tr1, pa);
tr := MtxMult(tr,tr1) ;
MtxMove(tr1, px,py) ;
tr := MtxMult(tr,tr1) ;
//
with sDef[-n-1] do begin
for o:=0 to mOrdN-1 do begin
o1 := mOrd[o].DataType ;
o2 := mOrd[o].DataNo ;
case (o1) of
2: begin
// 線分データ
with mLin[o2] do begin
ltp := Ltype ;
wid := line_width ;
MtxXY(lx1,ly1, start_x,start_y, tr);
MtxXY(lx2,ly2, end_x ,end_y , tr);
end;
MakeHatch4sub(col,ltp,wid, lx1,ly1,lx2,ly2,
wx1,wy1,wx2,wy2, pv1,w5,pv2,w6,w2,w4) ;
end;
end;
end;
end;
SetLength(zHLn, zHLnN);
zHCp := nil;
zHCpN:= 0;
end; |
取り合えずここではシンボル図形の線分データのみ対応としています。シンボル図形内の各データ毎に1つずつハッチング算出を行います。シンボル図形に尺度・回転をするため変換行列を使用しています。そして線分1本毎の具体的なハッチング線の算出は、MakeHatch4sub手続きにて行います。
| UnitData.pas |
// ハッチング(パターン) ハッチング線の算出 サブ
procedure TDataClass.MakeHatch4sub(col,ltp,wid:integer;
lx1,ly1,lx2,ly2,
wx1,wy1,wx2,wy2, pv1,pv1an,pv2,pv2an,py1,py2:double) ;
var
cx,cy,tl,lxc,lyc,w1,w2,w3,w4,w5,w6,w7,w8,n1,n2 : double ;
f1,f2 : Boolean ;
nn1,nn2,i,j : integer ;
begin
cx := (wx1+wx2)/2.0; // 対角中心点
cy := (wy1+wy2)/2.0;
lxc:= (lx1+lx2)/2.0; // 線中心点
lyc:= (ly1+ly2)/2.0;
Rev(w1,w2, cx,cy, lxc,lyc, -pv1an);
if (Abs(py1) > LIMIT8) then
n2 := Int( (w2-lyc)/py1 )
else
n2 := 0.0;
Rev(w1,w2, cx,cy, lxc,lyc, -pv2an);
if (Abs(py2) > LIMIT8) then
n1 := Int( (w2-lyc)/py2 )
else
n1 := 0.0;
lx1 := lx1 + pv2*n2*Cos(pv2an) + pv1*n1*Cos(pv1an);
ly1 := ly1 + pv2*n2*Sin(pv2an) + pv1*n1*Sin(pv1an);
lx2 := lx2 + pv2*n2*Cos(pv2an) + pv1*n1*Cos(pv1an);
ly2 := ly2 + pv2*n2*Sin(pv2an) + pv1*n1*Sin(pv1an);
lxc := (lx1+lx2)/2.0; // 線中心点
lyc := (ly1+ly2)/2.0;
wx1 := wx1 - Abs(lx2-lx1) ;
wy1 := wy1 - Abs(ly2-ly1) ;
wx2 := wx2 + Abs(lx2-lx1) ;
wy2 := wy2 + Abs(ly2-ly1) ;
tl := Dist(wx1,wy1,wx2,wy2); // 対角長さ
nn2 := 0 ;
f1 := True ;
while (f1) do begin
nn1 := 0 ;
f2 := True ;
while (f2) do begin
w1 := lxc + pv2*nn2*Cos(pv2an) + pv1*nn1*Cos(pv1an) ;
w2 := lyc + pv2*nn2*Sin(pv2an) + pv1*nn1*Sin(pv1an) ;
w3 := dAngle(lx2-lx1,ly2-ly1);
j := CalcHatch1Point(w1,w2,tl,w3); // 1ライン交点計算
w5 := w1 - Abs(lx2-lx1)/2.0 ;
w6 := w2 - Abs(ly2-ly1)/2.0 ;
w7 := w1 + Abs(lx2-lx1)/2.0 ;
w8 := w2 + Abs(ly2-ly1)/2.0 ;
if (Abs(w5-w7) < LIMIT10) then begin
w5 := w5 - LIMIT10 ;
w7 := w7 + LIMIT10 ;
end;
if (Abs(w6-w8) < LIMIT10) then begin
w6 := w6 - LIMIT10 ;
w8 := w8 + LIMIT10 ;
end;
for i:=0 to (j div 2)-1 do begin
w1 := zHCp[i*2 ].x ;
w2 := zHCp[i*2 ].y ;
w3 := zHCp[i*2+1].x ;
w4 := zHCp[i*2+1].y ;
if (ClipLine(w1,w2,w3,w4, w5,w6,w7,w8) = 2) then continue ;
if (zHLnN >= HATCH_LINE_MAX) then break ;
try
Inc(zHLnN);
if ((zHLnN mod 100) = 1) then SetLength(zHLn, zHLnN+99);
with zHLn[zHLnN-1] do begin
Color := col ;
Ltype := ltp ;
line_width := wid ;
x1 := w1 ;
y1 := w2 ;
x2 := w3 ;
y2 := w4 ;
end;
except
Dec(zHLnN);
f1 := False ;
f2 := False ;
break ;
end;
end;
if (nn1 >= 0) then
Inc(nn1)
else
Dec(nn1) ;
w1:=lxc+pv2*nn2*Cos(pv2an)+pv1*nn1*Cos(pv1an)-tl*Cos(pv2an);
w2:=lyc+pv2*nn2*Sin(pv2an)+pv1*nn1*Sin(pv1an)-tl*Sin(pv2an);
w3:=lxc+pv2*nn2*Cos(pv2an)+pv1*nn1*Cos(pv1an)+tl*Cos(pv2an);
w4:=lyc+pv2*nn2*Sin(pv2an)+pv1*nn1*Sin(pv1an)+tl*Sin(pv2an);
if (ClipPreLine(w1,w2,w3,w4, wx1,wy1,wx2,wy2) = 2) then begin
if (nn1 >= 0) then
nn1 := -1
else
f2 := False ;
end;
end;
if (nn2 >= 0) then
Inc(nn2)
else
Dec(nn2) ;
w1 := lxc + pv2*nn2*Cos(pv2an) - tl*Cos(pv1an);
w2 := lyc + pv2*nn2*Sin(pv2an) - tl*Sin(pv1an);
w3 := lxc + pv2*nn2*Cos(pv2an) + tl*Cos(pv1an);
w4 := lyc + pv2*nn2*Sin(pv2an) + tl*Sin(pv1an);
if (ClipPreLine(w1,w2,w3,w4, wx1,wy1,wx2,wy2) = 2) then begin
if (nn2 >= 0) then
nn2 := -1
else
f1 := False ;
end;
end;
end; |
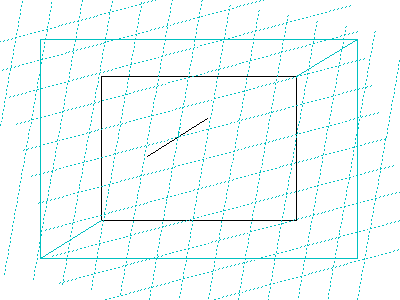
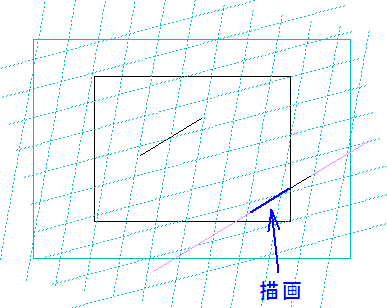
冒頭部は、シンボル図形の線を 配置位置がハッチング領域図形の外側にあるとハッチング処理が正常に出来ないため、パターンベクトルの整合性を取った上でハッチング領域図形内に移動する処理となっています。
wx1,wy1,wx2,wy2 はハッチング領域図形の境界ボックス範囲ですが、その範囲内でハッチング算出を行うとすると、線分の状態によっては、隅のほうで算出の漏れが生じてしまいます。そのため、線分の大きさの分、範囲を広げて算出を行うようにしています。
ハッチング(パターン)は、パターンベクトルによる繰り返し処理となりますが、そのパターンベクトルによる想定ラインと、この範囲とのクリッピング処理を想定し、クリッピング対象外となった場合に繰り返しを終了する、という風にしています。
なお、ハッチング線がかなり多くなってくると、メモリ不足ではなく、何故かスタックオーバーのエラーが出てしまうため、ハッチング線は最大20000本までと制限しています。この数値は今後変わってくるかもしれませんので定数宣言(HATCH_LINE_MAX)するようにしておきます。
それでは、ハッチング(パターン)の登録・描画のテストです。
| Unit1.pas |
・・・
// シンボル図形テスト
CData.AddDataTen( 'シンボルA', 1, 1,6, 0,0,0,5);
CData.AddDataLine('シンボルA', 1,10,1,1, -5,-5, 5,-5);
CData.AddDataLine('シンボルA', 1,11,1,1, 5,-5, 5, 5);
CData.AddDataLine('シンボルA', 1,12,1,1, 5, 5, -5, 5);
CData.AddDataLine('シンボルA', 1,13,1,1, -5, 5, -5,-5);
CData.AddDataLine('シンボルA', 1,14,1,1, -5,-5, 5, 5);
CData.AddDataLine('シンボルA', 1,15,1,1, -5, 5, 5,-5);
SetLength(lx,5);
SetLength(ly,5);
CData.AddCCurveDef(1,1,1,1,1); // 複合曲線定義 #1
lx[0] := 40; ly[0] := 40 ;
lx[1] := 140; ly[1] := 40 ;
lx[2] := 140; ly[2] := 140 ;
lx[3] := 40; ly[3] := 140 ;
lx[4] := 40; ly[4] := 40 ;
CData.AddCCrvDataLines(1,5,lx,ly); // 折線
CData.AddCCurveDef(2,2,2,6,1); // 複合曲線定義 #2
CData.AddCCrvDataArc(2,36,0, 90,130,8,0,180); // 円は円弧2つで形成
CData.AddCCrvDataArc(2,36,0, 90,130,8,180,0);
CData.AddCCurveDef(3,4,4,7,1); // 複合曲線定義 #3
lx[0] := 60; ly[0] := 60 ;
lx[1] := 90; ly[1] := 90 ;
lx[2] := 60; ly[2] := 120 ;
lx[3] := 60; ly[3] := 60 ;
CData.AddCCrvDataSpline(3,3,10,4,0,lx,ly); // スプライン曲線
CData.AddCCurveDef(4,5,5,8,1); // 複合曲線定義 #4
lx[0] := 120; ly[0] := 60 ;
lx[1] := 90; ly[1] := 90 ;
lx[2] := 120; ly[2] := 120 ;
lx[3] := 120; ly[3] := 60 ;
CData.AddCCrvDataSpline(4,3,10,4,0,lx,ly); // スプライン曲線
lx := nil;
ly := nil;
// ----- ハッチングテスト -----
// パターン
CData.AddDataHatch4('' ,'シンボルA', 1,2, 50.0,50.0,
15,0, 15,90, 1.0,1.0,0.0, 1,3,[2,3,4]);
CData.AddDataHatch4('部分図A','シンボルA', 1,2, 50.0,50.0,
15,0, 15,90, 1.0,1.0,0.0, 1,3,[2,3,4]);
DisplayAllData ; // 全データ表示
・・・ |
シンボル図形は「シンボルA」という名前で正方形に対角線2本を入れた図形、としています。ハッチング(パターン)での引数の 50.0,50.0 は、パターン(シンボル図形)の配置位置です。次の 15,0 がベクトル1の大きさ(15)と角度(0°)、次の 15,90 がベクトル2の大きさ(15)と角度(90°)です。これにおかしな値を入れないように注意して下さい。ハッチング線が大量状態となってハッチング線最大数になりハッチング領域図形全体にハッチングされない状態となります。
次の 1.0,1.0,0.0 は、配置するパターン(シンボル図形)の尺度X・尺度Y・角度[°]です。そのあとは、これまで同様、ハッチング領域を示す複合曲線定義の番号です。
これで描画をすると下記のような感じになります。
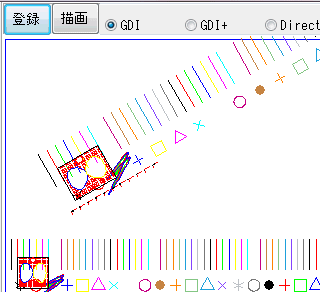
少し拡大します
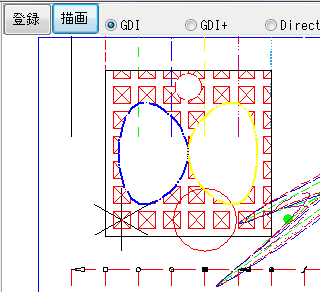
パターン(シンボル図形)を15°に傾けてみます。
| Unit1.pas |
・・・
CData.AddDataHatch4('' ,'シンボルA', 1,2, 50.0,50.0,
15,0, 15,90, 1.0,1.0,15.0, 1,3,[2,3,4]);
CData.AddDataHatch4('部分図A','シンボルA', 1,2, 50.0,50.0,
15,0, 15,90, 1.0,1.0,15.0, 1,3,[2,3,4]);
・・・ |
パターンベクトルを変えてみます。
| Unit1.pas |
・・・
CData.AddDataHatch4('' ,'シンボルA', 1,2, 50.0,50.0,
15,15, 15,75, 1.0,1.0,15.0, 1,3,[2,3,4]);
CData.AddDataHatch4('部分図A','シンボルA', 1,2, 50.0,50.0,
15,15, 15,75, 1.0,1.0,15.0, 1,3,[2,3,4]);
・・・ |
それでは、ここまでのテストプログラムです。実行ファイル、gdiplus.dll、gdipフォルダは入っていません。ソースのみです。
|
|
CAD装置(1)
CAD装置(2)
メディア
AutoCADの
DIESELマクロ
CSV
DXF
PCES
IGES
STEP
数学とCAD
CAD作ろ!
CADを考える
▲PREV
▼NEXT
M7
Jw_cad
|



