| �b�`�c���l����F�n�b�`���O(2) |
�O�ł̑����ŁA�n�b�`���O�ɂ��čl���܂��B
�O�łł̃n�b�`���O�̈�}�`�͕����A�����ł������ASXF�d�l�ł̃n�b�`���O�t�B�[�`���ł͕����Ȑ����~�ʁE�ȉ~�ʁE�ܐ��E�X�v���C���Ȑ��̏W�܂�ō\�������ƂȂ��Ă��܂��B�ܐ��͂��̂܂܂�����ǂ��Ƃ��āA�X�v���C���Ȑ����������w��ɂ������̏W�܂�Ƃ��ĕ\�����Ă��܂����炻����g�p����Ηǂ��̂ł����A�~�ʁE�ȉ~�ʂɂ��Ă͏����l���˂Ȃ�܂���B�܂�A�~�ʁE�ȉ~�ʂƂ��Čv�Z���s���̂��A����Ƃ��A��Ԑ����̏W�܂�Ƃ��Čv�Z���s���̂��A�ł��B�O�҂̏ꍇ�͓��R�A�����Ɖ~�i�~�ʁj�̌�_�v�Z�A�����Ƒȉ~�i�ȉ~�ʁj�̌�_�v�Z���K�{�ƂȂ��Ă��܂��B��������Ɠ��R�A�v���O�����͕��G�����܂��B�����A���m�Ɍv�Z���s���n�b�`���O���͐��������W�ŕ\�������ł��傤�B����ǂ��~�ʁE�ȉ~�ʂ͑��p�`��Ԃŕ\�������̂ŁA�n�b�`���O���͂͂ݏo�ĕ\������Ă��܂��\���͂���܂��B
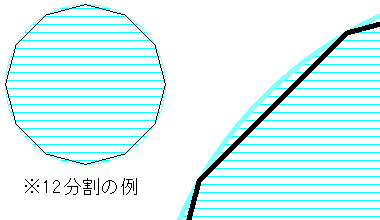
��҂̏ꍇ�́A�~�ʁE�ȉ~�ʂ̕����������ł���A�͂ݏo�ĕ\������鎖�͖����ł��傤����ǂ��A�����̕�Ԑ����Ƃ��Ĉ������߁A�v�Z�ʂ͑����Ȃ�܂��B���ɉ~�ʕ�������72�Ƃ���A72�{�̐����ł̌�_�v�Z�ƂȂ�܂��B�����������ɁA�ǂꂭ�炢�̑��x��������̂��H�Ƃ����͎̂��ۂɂ͂悭������܂���B�����Œ��ӂ��ׂ��Ȃ̂́A�~�ʁE�ȉ~�ʂ͌���A��ʔ{���ɂ���ĕ��������ς�邽�߁A��ʂ̊g��E�k��������s�x�A�n�b�`���O�v�Z���s��Ȃ��Ƃ����Ȃ��A�Ƃ������ł��B�n�b�`���O�̈�}�`�����G�ȏ�Ԃ�������f�[�^���ړ��e�����G�ȏ�Ԃ������ꍇ�A��ʂ�\�����邽�тɁ@�n�b�`���O�v�Z�����Ȃ������ĕ\���A�Ƃ������ɂȂ�ƁA�f�[�^�ʂ������Ȃ�Ȃ�قǁA�x���Ȃ��Ă�����������Ȃ��A�Ƃ����s���͂���܂��B�ƂȂ�A�������g�p�ʂ͑����Ă��܂��܂����A�n�b�`���O�v�f�f�[�^�ɁA�v�Z��̃n�b�`���O���̏W�܂�̃f�[�^���i�[����悤�ɂ��Ă����A�n�b�`���O�v�f�f�[�^���쐬�E�ύX�����ꍇ�ɂ��̓��e���X�V����悤�ɂ��āA�n�b�`���O�v�f�f�[�^��\������ꍇ�ɂ͉��x���v�Z����̂ł͂Ȃ��A���̌v�Z�ς̐����̏W�܂��\������悤�ɂ��Ă����A���x�I�Ɂ@�z��O�̒x��@�Ƃ����̂͂����炭�������Ȃ����낤�Ǝv���܂��B
�@
�����Ȃ��Ă���ƁA�~�ʁE�ȉ~�ʂ���ʔ{���ɂ���ĕ��������ς���Ă��܂��Ƃ����͕̂s�����Ƃ������ɂȂ�܂��̂ŁA�~�ʁE�ȉ~�ʂ̗v�f�f�[�^���ɕ������̃f�[�^���ڂ�lj����A������Q�Ƃ���悤�ɂ���A�Ƃ������ɂȂ炴��Ȃ��Ȃ�܂��B��������ύX�������Ȑ���`�v�f�̕ύX������Ɋւ��n�b�`���O�v�f�f�[�^�̕ύX���n�b�`���O���̎Z�o����ʂ̍č�}�A�Ƃ������ɂ͂Ȃ邾�낤�Ǝv���܂��B
�@
�Ƃ�����ŁA�{�v���O�����ł́A�����Ȑ���`���ꂽ�~�ʁE�ȉ~�ʂ��w�蕪�����ł̕�Ԑ����Ƃ��Ĉ����A�n�b�`���O�v�Z���s�����̂Ƃ��܂��B���̂��߁A�~�ʁE�ȉ~�ʗv�f�f�[�^�ɕ������̃f�[�^���ڂ�lj����܂��B�d�l���قȂ�Ƃ��������̂ʼn~�E�ȉ~�E�ʒ�/�p�x���@�E�o���[���v�f�f�[�^�����l�ɂ��Ă����܂��B
�@
| UnitData.pas |
�@�E�E�E
�@TDataCircle = record�@�@ // �v�f�^�\�L�v�f�b�~
�@�@exf : Boolean ;�@�@�@�@// ���݃t���O(True:�L��@False:����)
�@�@Layer : Integer ;�@�@�@// ���C��(1�`256)
�@�@Color : Integer ;�@�@�@// �F (0:���C���F�@ 1�`256)
�@�@Ltype : Integer ;�@�@�@// ����@(0:���C������ 1�`32)
�@�@line_width: Integer ;�@// �����@(0:���C������ 1�`16)
�@�@sep : Integer ;�@�@�@�@// ������(3�`3600)
�@�@Center_x : double ;�@�@// ���S�_�w���W
�@�@Center_y : double ;�@�@// ���S�_�x���W
�@�@Radius : double ;�@�@�@// ���a
�@end;
�@
�@TDataArc = record�@�@�@�@// �v�f�^�\�L�v�f�b�~��
�@�@exf : Boolean ;�@�@�@�@// ���݃t���O(True:�L��@False:����)
�@�@Layer : Integer ;�@�@�@// ���C��(1�`256)
�@�@Color : Integer ;�@�@�@// �F (0:���C���F�@ 1�`256)
�@�@Ltype : Integer ;�@�@�@// ����@(0:���C������ 1�`32)
�@�@line_width: Integer ;�@// �����@(0:���C������ 1�`16)
�@�@sep : Integer ;�@�@�@�@// ������(3�`3600)
�@�@Center_x : double ;�@�@// ���S�_�w���W
�@�@Center_y : double ;�@�@// ���S�_�x���W
�@�@Radius : double ;�@�@�@// ���a
�@�@Direction : Integer ;�@// �����@(0:�����v���,1:���v���)
�@�@start_angle : double ; // �n�p[��]
�@�@end_angle : double ;�@ // �I�p[��]
�@end;
�@
�@TDataEllipse = record�@�@// �v�f�^�\�L�v�f�b�ȉ~
�@�@exf : Boolean ;�@�@�@�@// ���݃t���O(True:�L��@False:����)
�@�@Layer : Integer ;�@�@�@// ���C��(1�`256)
�@�@Color : Integer ;�@�@�@// �F (0:���C���F�@ 1�`256)
�@�@Ltype : Integer ;�@�@�@// ����@(0:���C������ 1�`32)
�@�@line_width: Integer ;�@// �����@(0:���C������ 1�`16)
�@�@sep : Integer ;�@�@�@�@// ������(3�`3600)
�@�@Center_x : double ;�@�@// ���S�_�w���W
�@�@Center_y : double ;�@�@// ���S�_�x���W
�@�@Radius_x : double ;�@�@// �w�������a
�@�@Radius_y : double ;�@�@// �x�������a
�@�@rotation_angle:double; // ��]�p[��]
�@end;
�@
�@TDataEllipseArc = record // �v�f�^�\�L�v�f�b�ȉ~��
�@�@exf : Boolean ;�@�@�@�@// ���݃t���O(True:�L��@False:����)
�@�@Layer : Integer ;�@�@�@// ���C��(1�`256)
�@�@Color : Integer ;�@�@�@// �F (0:���C���F�@ 1�`256)
�@�@Ltype : Integer ;�@�@�@// ����@(0:���C������ 1�`32)
�@�@line_width: Integer ;�@// �����@(0:���C������ 1�`16)
�@�@sep : Integer ;�@�@�@�@// ������(3�`3600)
�@�@Center_x : double ;�@�@// ���S�_�w���W
�@�@Center_y : double ;�@�@// ���S�_�x���W
�@�@Radius_x : double ;�@�@// �w�������a
�@�@Radius_y : double ;�@�@// �x�������a
�@�@Direction: Integer ;�@ // �����@(0:�����v���,1:���v���)
�@�@rotation_angle:double; // ��]�p[��]
�@�@start_angle : double ; // �n�p[��]
�@�@end_angle : double ;�@ // �I�p[��]
�@end;
�@�E�E�E
�@TDataDimArc = record �@�@// �\�����v�f�b�ʒ����@�E�p�x���@
�@�@exf : Boolean ;�@�@�@�@// ���݃t���O(True:�L��@False:����)
�@�@Layer : Integer ;�@�@�@// ���C��(1�`256)
�@�@Color : Integer ;�@�@�@// �F (0:���C���F�@ 1�`256)
�@�@Ltype : Integer ;�@�@�@// ����@(0:���C������ 1�`32)
�@�@line_width: Integer ;�@// �����@(0:���C������ 1�`16)
�@�@sep : Integer ;�@�@�@�@// ������(3�`3600)
�@�@sun_x : double ;�@�@�@ // ���@�����_�w���W
�@�@sun_y : double ;�@�@�@ // ���@�����_�x���W
�@�@sun_radius : double ;�@// ���@�����a
�@�@sun_angle0 : double ;�@// ���@���n�p[��]
�@�@sun_angle1 : double ;�@// ���@���I�p[��]
�@�@�E�E�E
�@end;
�@�E�E�E
�@TDataDimBalloon = record // �\�����v�f�b�o���[��
�@�@exf : Boolean ;�@�@�@�@// ���݃t���O(True:�L��@False:����)
�@�@Layer : Integer ;�@�@�@// ���C��(1�`256)
�@�@Color : Integer ;�@�@�@// �F (0:���C���F�@ 1�`256)
�@�@Ltype : Integer ;�@�@�@// ����@(0:���C������ 1�`32)
�@�@line_width: Integer ;�@// �����@(0:���C������ 1�`16)
�@�@sep : Integer ;�@�@�@�@// ������(3�`3600)
�@�@vertex_number :integer; // ���_�� (2�`)
�@�@vertex_x : array of double ; // ���_�w���W
�@�@�E�E�E
�@end;
�@�E�E�E |
�f�[�^�\����ύX���܂����̂ŁA�e�f�[�^�lj��p�����ύX���Ă����܂��B
| UnitData.pas |
function AddDataCircle(s:string;lay,col,ltp,wid,sp:integer;
�@cx,cy,cr:double) : Boolean;
function AddDataArc(s:string;lay,col,ltp,wid,sp,dir:integer;
�@cx,cy,cr,sa,ea:double) : Boolean;
function AddDataEllipse(s:string;lay,col,ltp,wid,sp:integer;
�@cx,cy,rx,ry,ra:double) : Boolean;
function AddDataEllipseArc(s:string;lay,col,ltp,wid,sp,dir:integer;
�@cx,cy,rx,ry,ra,sa,ea:double) : Boolean;
�E�E�E
function AddDataDimArc(s,st:string;lay,col,ltp,wid,sp,f2,f3,f4,
�@ar11,ar12,ar21,ar22,fnt,bp,dir:integer;
�@sx,sy,sr,sa0,sa1, h1x0,h1y0,h1x1,h1y1,h1x2,h1y2,
�@h2x0,h2y0,h2x1,h2y1,h2x2,h2y2, ar1x,ar1y,ar1r, ar2x,ar2y,ar2r,
�@tx,ty,th,tw,ts,an,sl:double) : Boolean ;
function AddDataDimAngle(s,st:string;lay,col,ltp,wid,sp,f2,f3,f4,
�@ar11,ar12,ar21,ar22,fnt,bp,dir:integer;
�@sx,sy,sr,sa0,sa1, h1x0,h1y0,h1x1,h1y1,h1x2,h1y2,
�@h2x0,h2y0,h2x1,h2y1,h2x2,h2y2, ar1x,ar1y,ar1r, ar2x,ar2y,ar2r,
�@tx,ty,th,tw,ts,an,sl:double) : Boolean ;
�E�E�E
function AddDataDimBalloon(s,st:string;lay,col,ltp,wid,sp,fl,
�@num,ar,fnt,bp,dir:integer;vx,vy:array of double;
�@cx,cy,cr,arr, tx,ty,th,tw,ts,an,sl:double) : Boolean ;
�E�E�E
function AddCCrvDataArc(id,sp,dir:integer;
�@cx,cy,cr,sa,ea:double) : Boolean;
function AddCCrvDataEllipseArc(id,sp,dir:integer;
�@cx,cy,rx,ry,ra,sa,ea:double) : Boolean; |
�ܘ_�A��������
with dCir[dCirN-1] do begin
�@exf�@�@�@�@:= True ;
�@Layer�@�@�@:= lay ;
�@Color�@�@�@:= col ;
�@Ltype�@�@�@:= ltp ;
�@line_width := wid ;
�@sep�@�@�@�@:= sp ;
�@Center_x�@ := cx ;
�@Center_y�@ := cy ;
�@Radius�@�@ := cr ;
end; |
�̂悤�ɒlj�����悤�ɂ��܂��B���ɁA��ʕ\���̂ق����ύX���܂��B
| UnitDataGraph.pas |
procedure DisplayCircle(lay,col,ltp,wid,sp:integer;
�@px,py,pr:double;t:TMatrix);
procedure DisplayArc(lay,col,ltp,wid,sp,dir:integer;
�@px,py,pr,sa,ea:double;t:TMatrix);
procedure DisplayEllipse(lay,col,ltp,wid,sp:integer;
�@px,py,rx,ry,ra:double;t:TMatrix);
procedure DisplayEllipseArc(lay,col,ltp,wid,sp,dir:integer;
�@px,py,rx,ry,ra,sa,ea:double;t:TMatrix);
�@
procedure DisplayDimArc(lay,col,ltp,wid,sp,f2,f3,f4,
�@ar11,ar12,ar21,ar22,fnt,bp,dir:integer;
�@sx,sy,sr,sa0,sa1, h1x0,h1y0,h1x1,h1y1,h1x2,h1y2,
�@h2x0,h2y0,h2x1,h2y1,h2x2,h2y2, ar1x,ar1y,ar1r, ar2x,ar2y,ar2r,
�@tx,ty,th,tw,ts,an,sl:double;st:string;t:TMatrix);
procedure DisplayDimAngle(lay,col,ltp,wid,sp,f2,f3,f4,
�@ar11,ar12,ar21,ar22,fnt,bp,dir:integer;
�@sx,sy,sr,sa0,sa1, h1x0,h1y0,h1x1,h1y1,h1x2,h1y2,
�@h2x0,h2y0,h2x1,h2y1,h2x2,h2y2, ar1x,ar1y,ar1r, ar2x,ar2y,ar2r,
�@tx,ty,th,tw,ts,an,sl:double;st:string;t:TMatrix);
�@
procedure DisplayDimBalloon(lay,col,ltp,wid,sp,fl,
�@num,ar,fnt,bp,dir:integer;vx,vy:array of double;
�@cx,cy,cr, arr, tx,ty,th,tw,ts,an,sl:double;st:string;t:TMatrix); |
�_�}�[�J�̉~�́A72�����ŕ\������悤�ɂ��Ă����܂��B
�@
�Ⴆ�Ή~�̕`��͉��L�̂悤�ɂȂ�A�ȑO�ɔ�׃V���v���ɂȂ��Ă��܂��B
| UnitDataGraph.pas |
// �~�̕\��
procedure DisplayCircle(lay,col,ltp,wid,sp:integer;
�@px,py,pr:double;t:TMatrix);
var
�@c,cc,l,w, i,j : integer ;
�@ww, d1, a,aa, x1,y1,x2,y2,x3,y3,x4,y4 : double ;
�@fl : Boolean ;
begin
�@// �~�E�N���b�s���O�`�F�b�N
�@x1 := px-pr; y1 := py-pr; MtxXY(x1,y1, x1,y1, t);
�@x2 := px+pr; y2 := py-pr; MtxXY(x2,y2, x2,y2, t);
�@x3 := px+pr; y3 := py+pr; MtxXY(x3,y3, x3,y3, t);
�@x4 := px-pr; y4 := py+pr; MtxXY(x4,y4, x4,y4, t);
�@if (Clip4Point(x1,y1,x2,y2,x3,y3,x4,y4,
�@�@�@�@�@�@�@�@�@WndX1,WndY1,WndX2,WndY2) = 2) then exit;
�@
�@a := 2.0*Pi/sp ;
�@
�@DisplayLayCol2(lay,col,ltp,wid, c,cc,l,w,ww);
�@//
�@fl := False ;
�@if (CData.zLtp[l-1].Segment = 0)
�@ or(CData.zLtp[l-1].SpaceMax * mm_dot < 2.0)
�@ or(CData.zLtp[l-1].SpaceMax * mm_dot < ww ) then
�@�@fl := True ;
�@
�@i := 0 ;
�@d1 := 0.0 ;
�@aa := 0.0 ;
�@x1 := px + pr*Cos(aa);
�@y1 := py + pr*Sin(aa);
�@MtxXY(x1,y1, x1,y1, t);
�@for j:=1 to sp do begin
�@�@aa := aa + a;
�@�@x2 := px + pr*Cos(aa);
�@�@y2 := py + pr*Sin(aa);
�@�@MtxXY(x2,y2, x2,y2, t);
�@�@if (fl) then
�@�@�@DisplayLineSub1(x1,y1,x2,y2)
�@�@else
�@�@�@DisplayLineSub2(l,i,d1, x1,y1,x2,y2) ;
�@�@x1 := x2 ;
�@�@y1 := y2 ;
�@end;
end; |
�@
�ȏ�ɂ��A�~�E�~�ʁE�ȉ~�E�ȉ~�ʁE�ʒ����@�E�p�x���@�E�o���[���̊e�v�f�f�[�^����}����ۂɂ́A��������lj����Ďw�肷��悤�ɂȂ�܂����B
�@
���ɁA�n�b�`���O�̈�}�`��SXF�E�\�����v�f�́u�����Ȑ���`�v�ōs���܂����A�����Ȑ���`���ꂽ�ܐ��E�~�ʁE�ȉ~�ʁE�X�v���C���Ȑ��������Ɛڑ�����Ă��邩�ǂ����H�̃`�F�b�N���s���������ǂ��Ǝv���܂��̂ŁA���̃`�F�b�N�p�����쐬���鎖�ɂ��܂��B
�@
�v�f�f�[�^�o�^���Ƀ`�F�b�N������̂ł�����A�n�_�E�I�_�̍��W�������ƍ����Ă��邩�ǂ��������Ƀ`�F�b�N���Ă��������ł��̂ł���Ȃɓ������܂���B�uSXF Ver.3.1�����K��.pdf�v�ɂĈȉ��̂悤�ɋL�q����Ă��܂��B
1-11 �����Ȑ���`
�i1�j�����Ȑ��̕�����
�f�[�^�ێ�
�E�����Ȑ��̕��肷��ۂ�臒l�́A
�@�����Ł}0.0001 �o�i��_�Ԃ̋����j�܂łƂ���B |
�y��|�z
�E�����Ȑ����A�����̈���\�����Ă��邩�ۂ��̔��肪
�@CAD�\�t�g���ɈقȂ��Ă���ƁA�f�[�^�������ɕs�s����������B |
�Ƃ���܂��̂ŁA�����ł�����A
�@��(�I�_X�|���v�f�̎n�_X)2�{(�I�_Y�|���v�f�̎n�_Y)2
�̒l��0.001�ȉ��ł���n�j�A�Ƃ���Ηǂ��ł��傤�B�Ȃ��A�������̌v�Z�Œx���Ȃ邩������Ȃ��̂�
�@(�I�_X�|���v�f�̎n�_X)2�{(�I�_Y�|���v�f�̎n�_Y)2
�̒l��0.000001�ȉ��ł���n�j�A�ł��ǂ��ł��傤�B
�@
�����Ȑ���`���P���s���ۂɃ`�F�b�N������Ƃ������ł��ǂ���������܂��A�����ł́A�o�^�����Ă��܂��Ă���Ō�Ƀ`�F�b�N���s���A�Ƃ������ɂ��܂��B
�@
�Ȃ��A�����Ȑ���`���̗v�f�f�[�^�������悭����ł��炸�o���o����Ԃ̏ꍇ�́H�ƂȂ�A�ǂ����ŕ��בւ��̏������K�v�ɂȂ��Ă���Ǝv���܂����A�����I�ɁACAD����Ƃ��ĕ����Ȑ���`���s���Ƃ���A�ǂ̂悤�ȑ��������ł��傤���H�@�����炭�́A�P���v�f���N���b�N���Ă������@�ƁA�͈͑I����������@������ł��傤�B��������A���̎��Ƀ`�F�b�N�����בւ����s���ēo�^������Ηǂ��A�Ƃ��Ă��܂��A���i�K�̃f�[�^���x���ł̕��בւ��͕K�v�����ł��傤�B����ɁA�����Ȑ���`���̗v�f�f�[�^�̕��т��o���o���̏ꍇ�A��CAD�ւ����Ă������Ƃ��ɐ���ɏ�������邩�ǂ����H�Ƃ����s��������܂��B
| UnitData.pas |
// �����Ȑ���`���f�[�^�̐ڑ��`�F�b�N
// id : ID�ԍ�(1-)
// (ret) True:OK�@False:NG
function TDataClass.CCrvDataCheck(id:integer) : Boolean ; |
�@
�����Ȑ���`�Ńf�[�^�o�^�o����̂́A�ܐ��E�~�ʁE�ȉ~�ʁE�X�v���C���Ȑ��ł����A�Ⴆ�ΐ��������������ꍇ�ɂ́A�Q���_�̐ܐ��ɕϊ�����A�Ƃ����������K�v�ł��傤���A�~��ȉ~�����������ꍇ�́A�Q�̉~�ʁE�Q�̑ȉ~�ʂɕϊ����鏈���͕K�v�ɂȂ邾�낤�Ǝv���܂��B
�@
�@
���ɁA�����Ȑ���`�ɂ��\�������n�b�`���O�̈�}�`�͘A�������Ƃ��ĕ\��������ł����A�n�b�`���O�̈�������ϐ��͐�ɏq�ׂ��悤��
zHAr : array of TWorkHatchArea ; // ��Ɨp�b�n�b�`���O�̈�
zHArN: Integer ; |
�ł����A����͂P�̃n�b�`���O��`�悷��ۂɗ��p����ꎞ�I�ȍ�Ɨp�ϐ��ŁA�P�̐}�ʃf�[�^���ɂ͂P�̃n�b�`���O�̂ݑ��݁A�Ƃ������͋ɂ߂ċH�ł��̂ŁA���̕ϐ����ɉi���I�ɐ}�`�f�[�^���ێ������Ƃ������͂���܂���B
�@
�����Ȑ���`���s���A�ڑ��`�F�b�N���s���A�A�������f�[�^�����s���A���Ȍ����`�F�b�N���s���A�n�b�`���O�v�Z���s���A�n�b�`���O�`����s���A�Ƃ�������̒��ŁA�A�������f�[�^�����������̂��ǂ��ɓ����̂��A�Ƃ������ŁA�����Ȑ���`�f�[�^���ɕϐ���p�ӂ��Ă����ɓ���Ă����A�n�b�`���O�ŗ��p����ꍇ�ɂ͂��̓s�x�A�f�[�^�n��������A�Ƃ�����@������܂��B�܂��A��Ɨp�n�b�`���O�̈�ɒ��ړ����悤�ɂ����@������܂��B
�O�҂͊Ǘ����₷�����E�����Ȑ���`�f�[�^���p����ꍇ�ɂ͗L���ł��鎖�i�Ⴆ�A�قȂ�n�b�`���O���d�˂ĕ`�悷��ꍇ��A�������̒��ɍX�Ƀn�b�`���O���|����ꍇ�Ȃǁj�Ƃ��������b�g�͂���܂����A������������鎖�E�f�[�^�n��������K�v�����鎖�Ƃ����f�����b�g������܂��B
��҂͋t�ɁA�����Ȑ���`�f�[�^���p����ꍇ�́A���̓s�x�A�A�������f�[�^�����Ȃ����K�v�����鎖�E�����Ȃ�Ǝ��Ȍ����`�F�b�N���ēx�s���Ă��܂��\�������鎖�Ƃ����f�����b�g�͂��锽�ʁA�A�������f�[�^�p�������Ƃ��ĕK�v�͂Ȃ��Ƃ��������b�g�͂���܂��B
�v����ɁA�\���E�p�x�̖��Ȃ̂ł����A�e�n�b�`���O�f�[�^���Ƀn�b�`���O�����p�̃��������ʓr�K�v�ɂȂ��Ă��܂����A���܂�Ƀ�����������߂��Ă����ɂȂ�܂��̂ŁA�����́A��҂̃p�^�[�����Ƃ鎖�ɂ��܂��B
�@
���̍�Ƃ��s���O�ɁA�~�ʁE�ȉ~�ʁE�X�v���C���Ȑ���A�������f�[�^�ɕϊ�����葱���ɂ��čl���܂��B�����͊��ɁAUnitDataGraph.pas�ł� Display�`�Ƃ����葱���ŕ`��ł���悤�ɂȂ��Ă��܂����A�`�悻�̂��̂ƒ������Ă��邽�߁A�`��͂��Ȃ�����ǂ��A�������f�[�^���~�����Ƃ����ꍇ�ɂ͂��̂܂ܗ��p�o���܂���B�~�ʒ��x�Ȃ炻�̓s�x�v���O�����R�[�h�������Ă��債����Ƃł͂���܂����ɃX�v���C���Ȑ��Ƃ��Ȃ�ƍ�ƌ����������Ă��܂��܂��B��X���p���₷���悤�ɂ���p�̃��j�b�g UnitFuncCurve.pas �Ƃ��č���Ă����܂��B
�@
���F
| UnitDataGraph.pas |
// �~�̕\��
procedure DisplayCircle(lay,col,ltp,wid:integer;
�@px,py,pr:double;t:TMatrix);
�@�E�E�E
�@a := 2.0*Pi / n ;
�@
�@DisplayLayCol2(lay,col,ltp,wid, c,cc,l,w,ww);
�@//
�@fl := False ;
�@if (CData.zLtp[l-1].Segment = 0)
�@ or(CData.zLtp[l-1].SpaceMax * mm_dot < 2.0)
�@ or(CData.zLtp[l-1].SpaceMax * mm_dot < ww ) then
�@�@fl := True ;
�@
�@i := 0 ;
�@d1 := 0.0 ;
�@aa := 0.0 ;
�@x1 := px + pr*Cos(aa);
�@y1 := py + pr*Sin(aa);
�@MtxXY(x1,y1, x1,y1, t);
�@for j:=1 to Round(n) do begin
�@�@aa := aa + a;
�@�@x2 := px + pr*Cos(aa);
�@�@y2 := py + pr*Sin(aa);
�@�@MtxXY(x2,y2, x2,y2, t);
�@�@if (fl) then
�@�@�@DisplayLineSub1(x1,y1,x2,y2)
�@�@else
�@�@�@DisplayLineSub2(l,i,d1, x1,y1,x2,y2) ;
�@�@x1 := x2 ;
�@�@y1 := y2 ;
�@end;
end; |
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��
�V�F
| UnitDataGraph.pas |
// �~�̕\��
procedure DisplayCircle(lay,col,ltp,wid:integer;
�@px,py,pr:double;t:TMatrix);
�@�E�E�E
�@DisplayLayCol2(lay,col,ltp,wid, c,cc,l,w,ww);
�@//
�@fl := False ;
�@if (CData.zLtp[l-1].Segment = 0)
�@ or(CData.zLtp[l-1].SpaceMax * mm_dot < 2.0)
�@ or(CData.zLtp[l-1].SpaceMax * mm_dot < ww ) then
�@�@fl := True ;
�@
�@TransCircleToLines(sp,px,py,pr,t);
�@if (tLnsN = 0) then exit;
�@
�@i := 0 ;
�@d1 := 0.0 ;
�@x1 := tLns[0].x ;
�@y1 := tLns[0].y ;
�@for j:=1 to tLnsN-1 do begin
�@�@x2 := tLns[j].x ;
�@�@y2 := tLns[j].y ;
�@�@if (fl) then
�@�@�@DisplayLineSub1(x1,y1,x2,y2)
�@�@else
�@�@�@DisplayLineSub2(l,i,d1, x1,y1,x2,y2) ;
�@�@x1 := x2 ;
�@�@y1 := y2 ;
�@end;
�@
�@TransLnsClear ;
end; |
�@
| UnitFuncCurve.pas |
�E�E�E
var
�@tLns : array of TPointD ; // �ϊ������A�������f�[�^
�@tLnsN : integer ;
�@
�@procedure TransLnsClear ;
�@procedure TransCircleToLines(sp:integer;px,py,pr:double;t:TMatrix);
�@
implementation
�@
// �ϊ��A�������f�[�^�̃N���A
procedure TransLnsClear ;
begin
�@tLns := nil ;
�@tLnsN := 0 ;
end;
�@
// �~��A�������ɕϊ�
procedure TransCircleToLines(sp:integer;px,py,pr:double;t:TMatrix);
var
�@j : integer ;
�@a,aa, x1,y1 : double ;
begin
�@try
�@�@tLnsN := sp + 1 ;
�@�@SetLength(tLns, tLnsN);
�@except
�@�@TransLnsClear ;
�@�@exit ;
�@end;
�@
�@a := 2.0*Pi/sp ;
�@aa := 0.0 ;
�@for j:=0 to sp do begin
�@�@x1 := px + pr*Cos(aa);
�@�@y1 := py + pr*Sin(aa);
�@�@MtxXY(x1,y1, x1,y1, t);
�@�@tLns[j].x := x1 ;
�@�@tLns[j].y := y1 ;
�@�@aa := aa + a;
�@end;
end;
�@
end. |
�Q�i�K�ƂȂ�܂��̂ňꌩ�ʓ|��������܂��A�����悤�ȃv���O�����R�[�h���������͊y�ɂȂ�܂����A�����~�ł��A���������ňقȂ鎮�E��ԂɂȂ��Ă��܂��Ă���Ƃ����悤�Ȏ����Ȃ��Ȃ苤�ʐ������܂��B
�@
��L�̉~�Ɠ��l�ɁA�~�ʁE�ȉ~�E�ȉ~�ʁE�X�v���C���Ȑ��E�N���\�C�h�Ȑ��̏������s���悤�ɂ��܂��B�Ȃ��A�X�v���C���Ȑ��͊e���_�ɕϊ��s����|���Ă���v�Z���s���ĕ`����s���Ă��܂������A��L���j�b�g���ɂ��e�葱���̈��������ʉ����邽�߃X�v���C���Ȑ��ɂ��ϊ��s����w�肷��悤�ɂ������߁A�Z�o�����e���W�ɑ��ĕϊ��s����|����悤�d�l�ύX���Ă��܂��B�ܐ�������ɓ���o����悤�ɂ��Ă����܂��B
�@
| UnitFuncCurve.pas |
unit UnitFuncCurve;
�@
interface
�@
uses
�@Windows, UnitFunc ;
�@
var
�@tLns : array of TPointD ; // �ϊ������A�������f�[�^
�@tLnsN : integer ;
�@
�@procedure TransLnsClear ;
�@procedure TransLinesToLines(num:integer;vx,vy:array of double;
�@�@�@t:TMatrix);
�@procedure TransCircleToLines(sp:integer;px,py,pr:double;
�@�@�@t:TMatrix);
�@procedure TransArcToLines(sp,dir:integer;px,py,pr,sa,ea:double;
�@�@�@t:TMatrix);
�@procedure TransEllipseToLines(sp:integer;px,py,rx,ry,ra:double;
�@�@�@t:TMatrix);
�@procedure TransEllipseArcToLines(sp,dir:integer;px,py,rx,ry,ra,
�@�@�@sa,ea:double;t:TMatrix);
�@procedure TransBezierToLines(sp,num:integer;
�@�@�@vx,vy:array of double;t:TMatrix);
�@procedure TransBsplineToLines(oc,sp,num:integer;
�@�@�@vx,vy:array of double;t:TMatrix);
�@procedure TransSplineToLines(stp,oc,sp,num:integer;av:double;
�@�@�@vx,vy:array of double;t:TMatrix);
�@procedure TransClothoidToLines(dir,sp:integer;
�@�@�@bx,by,av,an,l1,l2:double;t:TMatrix); |
�@
����ł́A�����Ȑ���`�f�[�^����n�b�`���O�̈�}�`����������쐬���܂��B
| UnitData.pas |
// �����Ȑ���`���f�[�^����n�b�`���O�̈�}�`��
//�@ id : ID�ԍ�(1-)
//�@ no : �n�b�`���O�̈�}�`�ԍ�(1-)
// (ret) True:OK�@False:NG
// ���n�b�`���O�̈�}�` zHAr,zHArN �͗\�߃Z�b�g�E�������m��
function TDataClass.CCrvDataToHAr(id,no:integer) : Boolean ; |
����ɂ��A�n�b�`���O�̈�}�`�p�̘A�������f�[�^�����邱�Ƃ��o���܂��̂ŁA����𗘗p���ăn�b�`���O�̃e�X�g���s���Ă݂܂��B
�@
| Unit1.pas |
SetLength(lx,5);
SetLength(ly,5);
CData.AddCCurveDef(1,1,1,1,1); // �����Ȑ���` #1
lx[0] := 40; ly[0] := 40 ;
lx[1] := 140; ly[1] := 40 ;
lx[2] := 140; ly[2] := 140 ;
lx[3] := 40; ly[3] := 140 ;
lx[4] := 40; ly[4] := 40 ;
CData.AddCCrvDataLines(1,5,lx,ly); // �ܐ�
�@
CData.AddCCurveDef(2,1,1,1,1); // �����Ȑ���` #2
lx[0] := 60; ly[0] := 60 ;
lx[1] := 60; ly[1] := 100 ;
lx[2] := 100; ly[2] := 100 ;
lx[3] := 100; ly[3] := 60 ;
lx[4] := 60; ly[4] := 60 ;
CData.AddCCrvDataLines(2,5,lx,ly); // �ܐ�
�@
CData.AddCCurveDef(3,1,1,1,1); // �����Ȑ���` #3
lx[0] := 110; ly[0] := 50 ;
lx[1] := 130; ly[1] := 90 ;
lx[2] := 110; ly[2] := 130 ;
lx[3] := 110; ly[3] := 50 ;
CData.AddCCrvDataLines(3,4,lx,ly); // �ܐ�
�@
CData.AddCCurveDef(4,1,1,1,1); // �����Ȑ���` #4
CData.AddCCrvDataArc(4,36,0, 80,120,15,0,180);
CData.AddCCrvDataArc(4,36,0, 80,120,15,180,0);
�@
lx := nil;
ly := nil;
�@
// ----- �n�b�`���O�e�X�g -----
�@
// �n�b�`���O�̈�}�`�̃Z�b�g
CData.zHArN := 4 ;
SetLength(CData.zHAr,CData.zHArN);
CData.CCrvDataToHAr(1,1); // �����Ȑ���` #1 �� �O�s��
CData.CCrvDataToHAr(2,2); // �����Ȑ���` #2 �� ����1
CData.CCrvDataToHAr(3,3); // �����Ȑ���` #3 �� ����2
CData.CCrvDataToHAr(4,4); // �����Ȑ���` #4 �� ����3
// min,max���擾
�E�E�E |
�@
�n�b�`���O�̍�}�e�X�g�ł��B�܂��v�f�f�[�^���͍s���Ă��܂���B
�����Ȃ�܂��̂ŁA��荇�����͂����܂łɂ��Ă����܂��B
�@
�@
����ł́A�����܂ł̃e�X�g�v���O�����ł��B���s�t�@�C���Agdiplus.dll�Agdip�t�H���_�͓����Ă��܂���B�\�[�X�݂̂ł��B
�@
|



